树型动态规划-括号树

P5658

题目背景

本题中合法括号串的定义如下：

本题中子串与不同的子串的定义如下：

字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 ll与终止位置 r 来表示，记为 S(l,r)（1≤l≤r≤∣S∣，∣S∣ 表示 S 的长度）。
S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 ll不同或 r不同。

一个大小为 n 的树包含 n个结点和 n−1 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 n 的树，树上结点从 1∼n编号，1 号结点为树的根。除 11号结点外，每个结点有一个父亲结点，u（2≤u≤n）号结点的父亲为 fu（1≤fu<u）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 si 为：将根结点到 ii号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 sisi是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 i（1≤i≤n）求出，sis 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 sisi共有 ki个不同子串是合法括号串，你只需要告诉小 Q 所有 i×ki的异或和，即：

(1×k1) xor (2×k2) xor (3×k3) xor ⋯ xor (n×kn)

其中 xor是位异或运算。

第一行一个整数 n，表示树的大小。

第二行一个长为 n 的由( 与) 组成的括号串，第 i个括号表示 i 号结点上的括号。

第三行包含 n−1 个整数，第 i（1≤i<n）个整数表示 i+1号结点的父亲编号 fi+1。

仅一行一个整数表示答案。

输入 #1

5 
(()() 
1 1 2 2

输出 #

【样例解释1】

树的形态如下图：

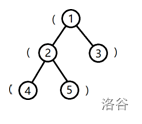
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 00。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 0。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 1。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 0。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 1。

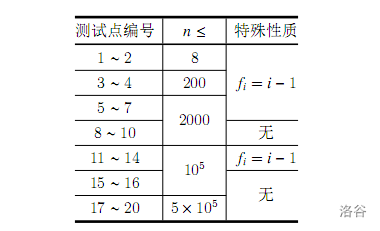
【数据范围】

解题思路：

这道题的核心是如何计算从根节点到每个节点形成的括号串中有多少个不同的合法子串。合法括号串的定义已在题目中给出。

我们可以用DFS来遍历树，过程中维护一个栈来跟踪路径上未匹配的(，以及一个数组lst来记录从根节点到当前节点的合法括号子串的数量。DFS过程中，我们对每个节点进行如下处理：

如果当前节点是(：
- 将节点索引压入栈中，用来匹配后续的)。
如果当前节点是)：
- 如果栈不为空，说明有匹配的(：
  - 弹出栈顶元素，找到与当前)匹配的(的索引。
  - 利用lst数组更新当前节点的合法子串数。
  - 同时更新栈的状态，以便于继续处理其他节点。
记录累加的合法括号子串数：
- 对于每个节点，用sum数组记录从根节点到当前节点的所有合法括号子串的累积数。
计算最终的异或和：
- 遍历所有节点，计算i * k_i的值（其中k_i是节点i的合法子串数），并将这些值进行异或运算，得出最终结果。