树的存储结构

一、父亲表示法

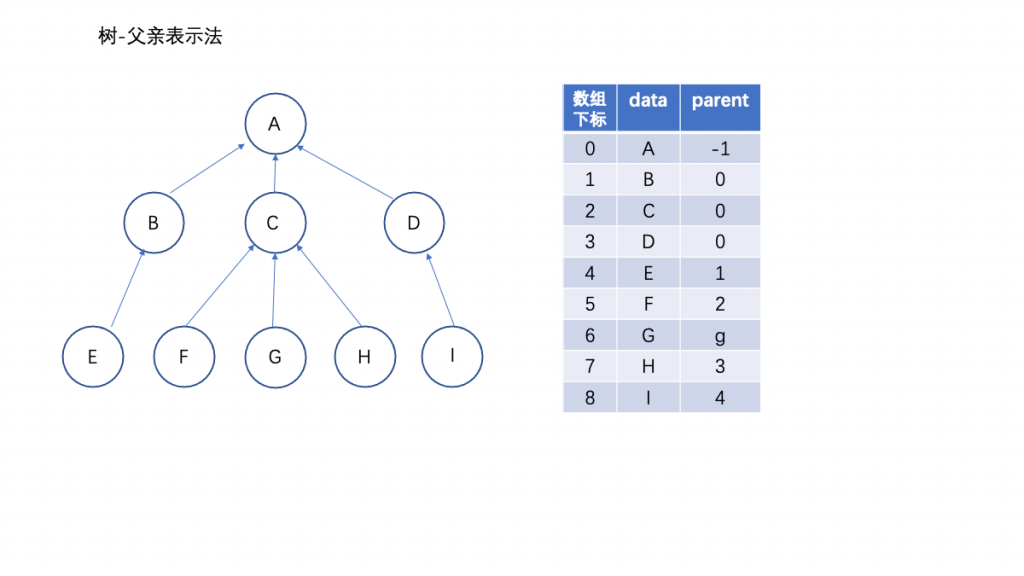
原理：利用一维数组来表示树,一维数组的每个元素表示树的结点,其中包括结点的数据和该结点的双亲在数组中的下标；数组中的第一个元素表示根结点,该结点无双亲,因此parent域用-1表示,其他结点按照层序存储.如结点B、 C、D 的双亲结点是下标为0的根结点,其parent域用0表示。
优缺点：利用了树中除根结点外每个结点都有唯一的父结点这个性质。很容易找到树根，但找孩子时需要遍历整个线性表。

#include <iostream>
using namespace std;

struct Node{
    char data;
    int parent;
};

int main(){
    int n;
    cin>>n;
    Node tree[n];

    for(int i=0;i<n;i++){
        cin>>tree[i].data;
        cin>>tree[i].parent;
    }

    for(int i=0;i<n;i++){
        cout<<tree[i].data;
        cout<<' ';
        cout<<tree[i].parent;
        cout<<endl;
    }
}

二、孩子表示法

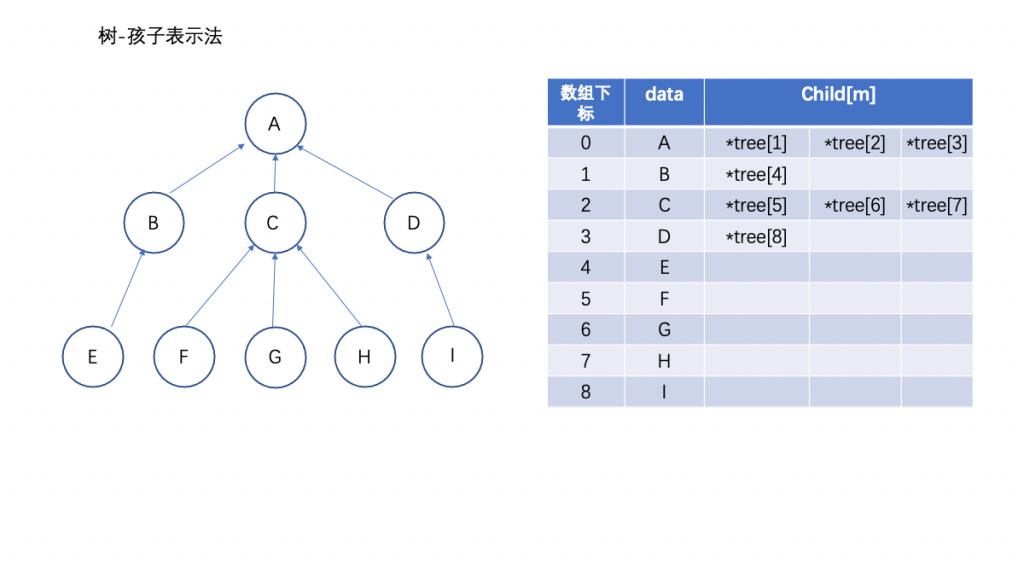
孩子表示法存储普通树采用的是 “顺序表+链表/数组” 的组合结构，其存储过程是：从树的根节点开始，使用顺序表依次存储树中各个节点，需要注意的是，与双亲表示法不同，孩子表示法会给各个节点配备一个链表或指针数组，用于存储各节点的孩子节点位于顺序表中的位置。

#include<iostream>
using namespace std;
const int m = 10;           //树的度

struct node
{
    char data;             //数据域
    node* child[m];          //指针域，指向若干孩子结点
};

int main(){
    int n;
    cin>>n;
    node tree[n];
    tree[0].data='A';
    tree[0].child[0]=&tree[1];
    tree[1].data='B';
    cout<<tree[0].child[0]<<endl;
    cout<<&tree[1];
    return 0;
}

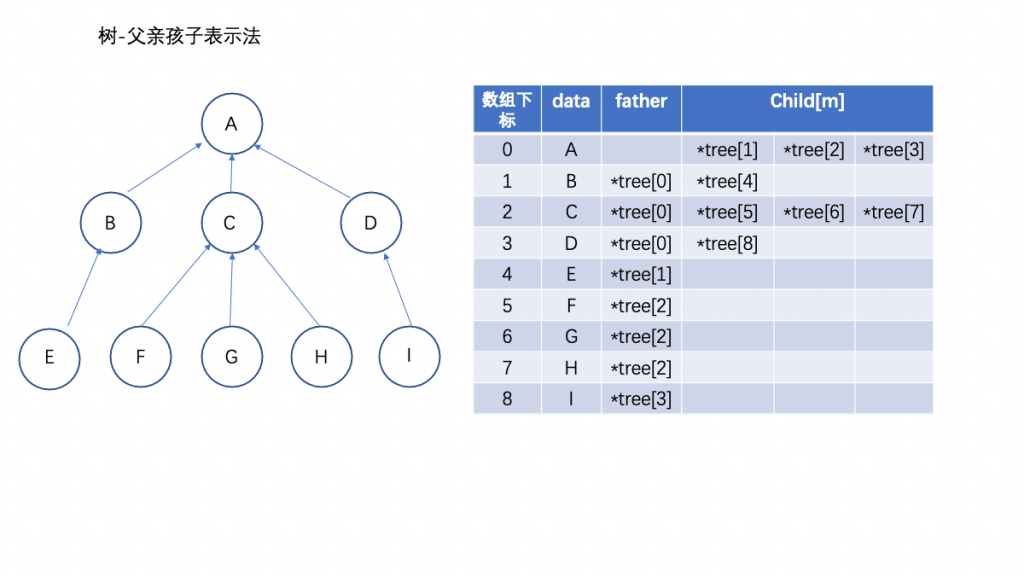
三、父亲孩子表示法

#include<iostream>
using namespace std;
const int m = 10;           //树的度

struct node
{
    char data;             //数据域
    node *child[m];       //指针域，指向若干孩子结点
    node  *father;
};

int main(){
    int n;
    cin>>n;
    node tree[n];
    tree[0].data='A';
    tree[0].child[0]=&tree[1];
    tree[1].data='B';
    tree[1].father=&tree[0];
    cout<<tree[1].father<<endl;
    cout<<&tree[0];
    return 0;
}

四、孩子兄弟表示法

树结构中，位于同一层的节点之间互为兄弟节点。例如，图 1 的普通树中，节点 A、B 和 C 互为兄弟节点，而节点 D、E 和 F 也互为兄弟节点。
孩子兄弟表示法，采用的是链式存储结构，其存储树的实现思想是：从树的根节点开始，依次用链表存储各个节点的孩子节点和兄弟节点。

因此，该链表中的节点应包含以下 3 部分内容（如图 2 所示）：
1、节点的值；
2、指向第一个孩子节点的指针；
3、指向相邻右兄弟节点的指针；

struct Node{ 
       char  data; 
       Node * firstchild,*nextsibling; 
};

习题：

找树根和孩子
【问题描述】　　给定一棵树，输出树的根root，孩子最多的结点max以及他的孩子
【输入格式】　　第一行：n（结点数<=100），m（边数<=200）。以下m行；每行两个结点x和y，表示y是x的孩子(x,y<=1000)。
【输出格式】第一行：树根：root。第二行：孩子最多的结点max。　　第三行：max的孩子。

【输入样例】
8 7
4 1
4 2
1 3
1 5
2 6
2 7
2 8

输出样例
4
2
6 7 8

Previous Topic

Back to Lesson

Next Topic

数据结构与算法

树的存储结构