二叉树的遍历
适用级别:普及组
难度系数:4
深度优先遍历(Depth First Traversals ):
1、前序遍历(Preorder):先访问根结点,然后再前序遍历左子树,再前序遍历右子树(Root,Left,Right)
2、中序遍历(Inorder):先遍历根结点的左子树,然后是访问根结点,最后遍历右子树(Left,Root,Right)
3、后序遍历(Postorder):从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点(Left,Right,Root)
广度优先遍历(Breadth First Traversals ):
层序遍历(Level Order ):从根结点从上往下逐层遍历,在同一层,按从左到右的顺序对结点访问
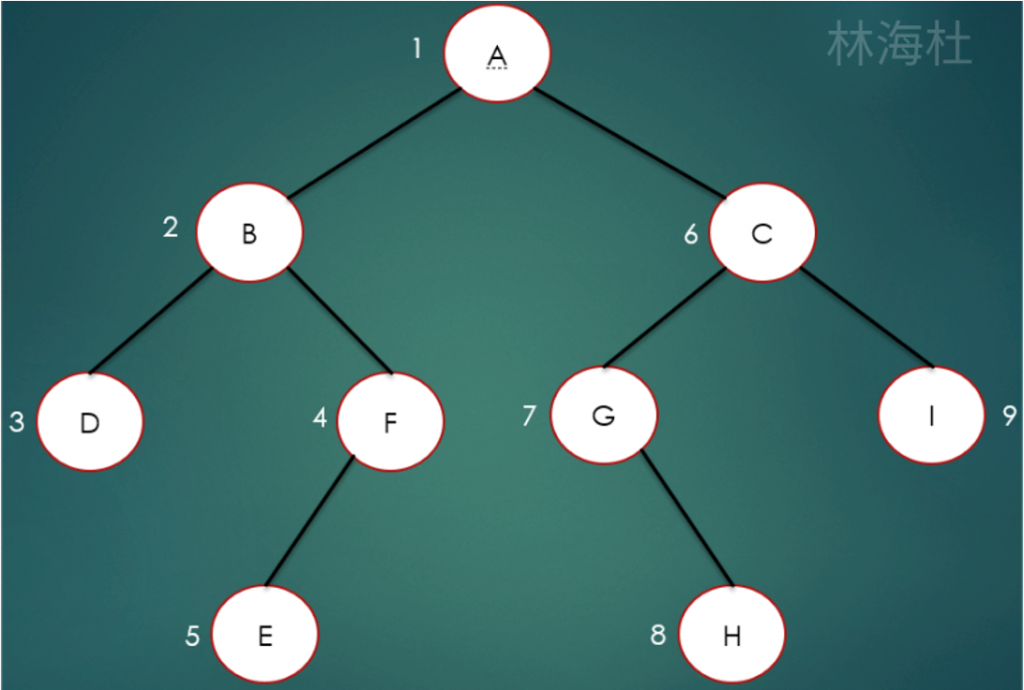
树的四种遍历方式
前序遍历结果为:ABDFECGHI
中序遍历结果为:DBEFAGHCI
后序遍历结果为:DEFBHGICA
层序遍历结果为:ABCDFGIEH
树的深度遍历代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | /**************************************************************** C++ tree_DFT author: Alex Li date: 2023-6-3 version:1.5 ****************************************************************/ #include <iostream> using namespace std; struct Node{ int data; struct Node *left, *right; }; Node* newNode(int data){ Node* temp=new Node; temp->data=data; temp->left=NULL; temp->right=NULL; return temp; } void printInorder(struct Node* node){ if(node==NULL) return; printInorder(node->left); cout<<node->data<<" "; printInorder(node->right); } void printPreorder(struct Node* node){ if(node==NULL) return; cout<<node->data<<" "; printPreorder(node->left); printPreorder(node->right); } void printPostorder(struct Node* node){ if(node==NULL) return; printPostorder(node->left); printPostorder(node->right); cout<<node->data<<" "; } int main(){ struct Node* root=newNode(1); root->left=newNode(2); root->right=newNode(3); root->left->left=newNode(4); root->left->right=newNode(5); cout << "\nPreorder traversal of binary tree is \n"; printPreorder(root); cout << "\nInorder traversal of binary tree is \n"; printInorder(root); cout << "\nPostorder traversal of binary tree is \n"; printPostorder(root); return 0; } |
广度优先遍历代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | /**************************************************************** * C++ for binary tree DFS * author : Alex Li * date: 2023-6-3 * version:1.0 *****************************************************************/ #include <iostream> using namespace std; // A binary tree node has data,pointer to left child and a pointer to right child struct node { int data; node *left, *right; }; /* Compute the "height" of a tree -- the number ofnodes along the longest path from the root node down to the farthest leaf node.*/ int height(node* node){ if (node == NULL) return 0; else { //compute the height of each subtree int lheight = height(node->left); int rheight = height(node->right); //use the larger one if (lheight > rheight) return (lheight + 1); else return (rheight + 1); } } // Print nodes at a current level void printCurrentLevel(node* root, int level){ if (root == NULL) return; if (level == 1) cout << root->data << " "; else if (level > 1) { printCurrentLevel(root->left, level - 1); printCurrentLevel(root->right, level - 1); } } // Function to print level order traversal a tree void printLevelOrder(node* root){ int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // newNode function that allocates a new node with the given data and NULL left and right pointers. node* newNode(int data){ node* Node = new node(); Node->data = data; Node->left = NULL; Node->right = NULL; return (Node); } // Driver code int main(){ node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout << "Level Order traversal of binary tree is "; printLevelOrder(root); return 0; } |
洛谷:U0306/P1827 P1030 B3642