简单选择排序(Selection Sort)
适用组别:入门级
难度系数:3
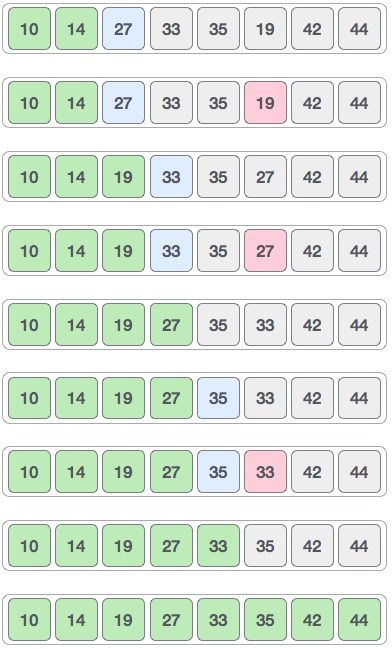
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2.1 算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
初始状态:无序区为R[1..n],有序区为空;
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;n-1趟结束,数组有序化了。







代码实现一:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | /**************************************************************** * Description: select sort by C++ * Author: Alex Li * Date: 2023-05-31 17:22:04 * LastEditTime: 2023-06-17 22:09:40 ****************************************************************/ #include <iostream> using namespace std; int a[1000]; int main (){ int i = 0, n; cin >> n; do{ cin >> a[i]; i++; }while (i < n); for (int k = 0; k < n - 1; ++k){ for (int j = k; j < n - 1; ++j){ if (a[k] > a[j + 1])swap(a[k],a[j+1]); } } for (int l = 0; l < n; ++l){ cout << a[l] <<' '; } return 0; } |
代码实现二:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | /**************************************************************** * Description: select sort by C++ * Author: Alex Li * Date: 2023-05-31 17:22:04 * LastEditTime: 2023-06-17 22:16:14 ****************************************************************/ #include <iostream> using namespace std; int arr[1000]; int main (){ int i = 0,n,min_index;; cin >> n; do{ cin >>arr[i]; i++; }while (i < n); for (int k = 0; k < n - 1; ++k){ min_index=k; for (int j = k+1; j < n; ++j){ if (arr[min_index] >arr[j])min_index=j; } if(min_index!=k)swap(arr[min_index],arr[k]); } for (int l = 0; l < n; ++l){ cout << arr[l] <<' '; } return 0; } |