算法的复杂度(algorithm complexity)
适用组别:提高组
难度系数:6
算法的时间复杂度(Algorithm time complexity)
一个程序或算法的时间效率,也称”时间复杂度”,有时简称”复杂度”。
复杂度常用大写的字母O和小写字母n来表示,比如O(n), O(n^2)等。n代表问题的规模。
时间复杂度是用算法运行过程中,某种时间固定的操作需要被执行的次数和n的关系来度量的。在无序数列中查找某个数,复杂度是O(n)。
计算复杂度的时候,只统计次数最多的(n足够大时)那种固定操作的次数。比如某个算法需要执行加法n^2次,除法n次,那么就记其复杂度为O(n^2)的。
复杂度有”平均复杂度”和”最坏复杂度”两种,两者可能一致,也可能不一致。
1、常数复杂度:O(1)
下面代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,是一个常数。那么无论这类代码有多长,都可以用O(1)来表示它的时间复杂度。
1 2 3 4 5 6 7 8 | #include <iostream> using namespace std; int main(){ int n; cin>>n; n=n+1000; //常数O(1) cout<<n; } |
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream> using namespace std; int main(){ int n; cin>>n; cout<<n*(n+1)/2; //常数O(1) for(int i=0;i<=10;i++){ cout<<n*n; } cout<<n; } |
2、线性复杂度:O(n)
下面代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化线性变化,因此这类代码都可以用O(n)来表示它的时间复杂度。
例如在无序数列中查找某个数(顺序查找) 。
1 2 3 4 5 6 7 8 9 | #include <iostream> using namespace std; int main(){ int n,sum=0; cin>>n; For (int i = 1; i <=n; i++) sum+=i; //执行了n次O(n) cout<<sum; } |
1 2 3 4 5 6 7 8 9 | #include <iostream> using namespace std; int main(){ int n,sum=0; cin>>n; For (int i = 1; i <=3*n; i++) sum+=i; //执行了n次O(n) cout<<sum; } |
3、对数复杂度:O(logn)
对数最常出现的规律为:如果一个算法用常数时间将问题的大小削减为其一部分(通常为1/2),那么该算法的时间复杂度为O(log N)。
二分查找的复杂度就是对数复杂度。
int number=1;
while(number<n){
number=number*2; //时间复杂度为O(logn)的算法
}
while(n>1){
n=n/3; //时间复杂度为O(logn)的算法
}
4、乘积复杂度O(n*m)
由两个参数乘积决定算法复杂度
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream> using namespace std; int main(){ int n, m,s=0; cin>>n>>m; for (int i = 0; i <n; i++){ for (int j = 0; j <m; j++){ s++; } } } |
5、平方阶复杂度: O(n²)
冒泡排序、插入排序、选择排序都是这种复杂度,平面上有n个点,要求出任意两点之间的距离 。
for(int i=1;i<=n;i++){
for(int j=1;j<=n;i++){
cout<<i+j;
}
}
int sum=0;
for (int i = 1; i <=n; i++){
for (int j =1; j <=i; j++){
sum++;
}
}
O(n3)
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++)
cout<<i+j+k;
}
}
}
6、线性对数阶O(nlogn)
快速排序,归并排序是这种复杂度
for(m=1; m<n; m++) {
i = 1;
while(i<n) {
i = i * 2;
}
}
7、指数复杂度:O(a^n)
8、阶乘复杂度:O(n!)
如果复杂度是多个n的函数之和,则只关系随n的增长,结果增长最快的哪个函数。
O(n^3+n^2)==O(n^3)
O(2^n+n^3)=O(2^n)
O(n!+3^n)=O(n!)
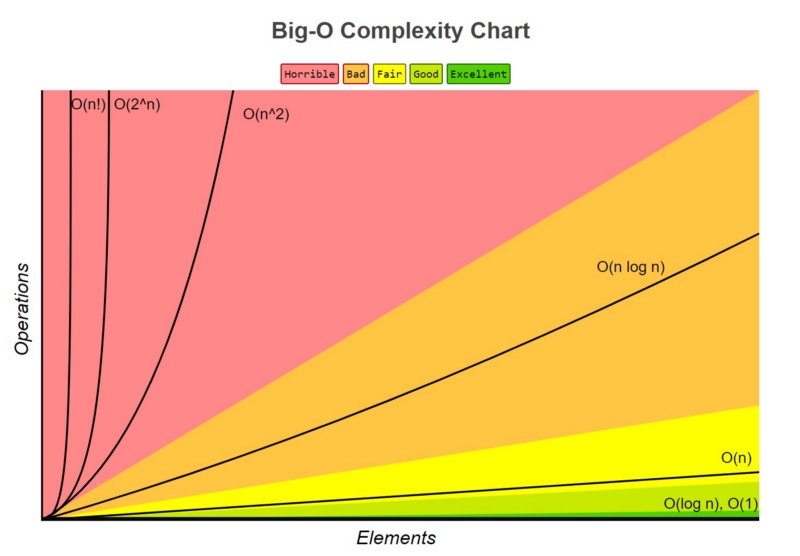
复杂度大小顺序:
O(n!)>O(2^n)>O(n^2)>O(nlogn)>O(n)>O(logn)>O(1)
算法的空间复杂度
空间复杂度(algorithm Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,是表示存储空间与输入值 之间的关系。
1.常数,记作O(1)
int n; cin>>n; cout<<++n;
int n,m=0; cin>>n; for(int i;i<n;i++) m+=i;
2,线性相关,O(n)
vector<int> a; int n; cin>>n; for(int i=0;i<n;i++) a.push_back(i);
3.递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间
long long Factorial(int N) {
if(n=2)return 2;
Factorial(N-1)*N;
}
总结:
大多数情况下时间复杂度和空间复杂度只能选一个最好,也就是通常说是的空间换时间。
| 类型 | 算法 | 时间复杂(平均) | 时间复杂度最坏(最坏) | 时间复杂度(最优) | 空间复杂度 | 稳定性 |
| 插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 | |
| 比 | 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 |
| 较 | 选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 类 | 希尔排序 | O(n1.3) | O(n2) | O(n) | O(1) | 不稳定 |
| 快速排序 | O(nlog_2n) | O(n2) | O(nlog_2n) | O(nlog_2n) | 不稳定 | |
| 归并排序 | O(nlog_2n) | O(nlog_2n) | O(nlog_2n) | O(n) | 稳定 | |
| 堆排序 | O(nlog_2n) | O(nlog_2n) | O(nlog_2n) | O(1) | 不稳定 | |
| 非 | 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 比 | 桶排序 | O(n+k) | O(n2) | O(n) | O(n+k) | 稳定 |
| 较 | 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |