小测验-排列组合
Quiz Summary
0 of 14 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 14 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 14
1. Question
1、设字符串 S=Olympic,S 的非空子串的数目是( )。 (2008年真题)
CorrectIncorrect -
Question 2 of 14
2. Question
2、将数组{8,23,4,16,77,−5,53,100} 中的元素按从大到小的顺序排列,每次可以交换任意两个元素,最少需要交换( )次。 (2008年真题)
CorrectIncorrect -
Question 3 of 14
3. Question
3、原字符串中任意一段连续的字符所组成的新字符串称为子串。则字符 AAABBBCCC 共有( )个不同的非空子串。 (2012年普及组)
CorrectIncorrect -
Question 4 of 14
4. Question
4、(子集划分)将 n 个数 (1,2,…,n) 划分成 r 个子集。每个数都恰好属于一个子集,任何两个不同的子集没有共同的数,也没有空集。将不同划分方法的总数记为S(n,r)。例如,S(4,2)=7,这 7 种不同的划分方法依次为 {(1),(234)}, {(2),(134)}, {(3),(124)}, {(4),(123)}, {(12),(34)}, {(13),(24)}, {(14),(23)} 。(2007年真题)
-
当 n=6,r=3 时,S(6,3)=
CorrectIncorrect -
-
Question 5 of 14
5. Question
5、给定 n 个有标号的球,标号依次为 1,2,…,n。将这 n 个球放入 r 个相同的盒子里,不允许有空盒,其不同放置方法的总数记为 S(n,r)。例如,(4,2)=7S(4,2)=7,这 77 种不同的放置方法依次为 {(1),(234)},{(2),(134)},{(3),(124)},{(4),(123)},{(12),(34)},{(13),(24)},{(14),(23)}。当 n=7,r=4 时,S(7,4)=? (2007年提高组)
-
S(7,4)=
CorrectIncorrect -
-
Question 6 of 14
6. Question
6、书架上有 4 本不同的书 A、B、C、D。其中 A 和 B 是红皮的,C 和 D 是黑皮的。把这 4 本书摆在书架上,满足所有黑皮的书都排在一起的摆法有_____种。满足 A 必须比 C 靠左,所有红皮的书要摆放在一起,所有黑皮的书要摆放在一起,共有______种摆法。
-
第一空
第二空
CorrectIncorrect -
-
Question 7 of 14
7. Question
7、有 6 个城市,任何两个城市之间都有一条道路连接,6 个城市两两之间的距离如下表所示,则城市 1 到城市 6 的最短距离为_____________。
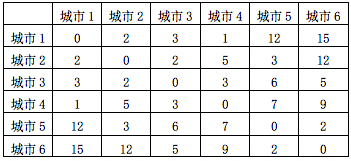
-
答案为
CorrectIncorrect -
-
Question 8 of 14
8. Question
8、(最短路线)某城市的街道是一个很规整的矩形网络(见下图),有 7 条南北向的纵街,5 条东西向的横街。现要从西南角的 A 走到东北角的 B 。(2007年真题)
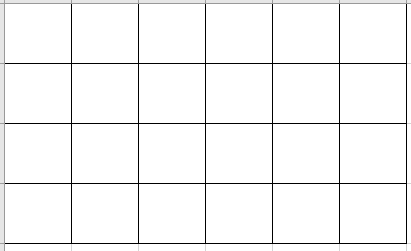
-
最短的走法共有多少种?
CorrectIncorrect -
-
Question 9 of 14
9. Question
9、书架上有 21 本书,编号从 1 到 21,从其中选 4 本,其中每两本的编号都不相邻的选法一共有______种。 (2008年真题)
-
共有
CorrectIncorrect -
-
Question 10 of 14
10. Question
10、小陈现有 2 个任务 A,B 要完成,每个任务分别有若干步骤如下:A=a1→a2→a3,B=b1→b2→b3→b4→b5。在任何时候,小陈只能专心做某个任务的一个步骤。但是如果愿意,他可以在做完手中任务的当前步骤后,切换至另一个任务,从上次此任务第一个未做的步骤继续。每个任务的步骤顺序不能打乱,例如 ⋯→a2→b2→a3→b3→… 是合法的,而 ⋯→a2→b3→a3→b2… 是不合法的。小陈从 B 任务的b1 步骤开始做,当恰做完某个任务的某个步骤后,就停工回家吃饭了。当他回来时,只记得自己已经完成了整个任务 A,其他的都忘了。试计算小陈饭前已做的可能的任务步骤序列共有( )种。 (2009年真题)
-
共有 种
CorrectIncorrect -
-
Question 11 of 14
11. Question
11、每份考卷都有一个 8 位二进制序列号。当且仅当一个序列号含有偶数个 1 时,它才是有效的。例如,00000000、01010011都是有效的序列号,而 11111110 不是。那么,有效的序列号共有_____个。(2011年普及组)
-
正确答案:
CorrectIncorrect -
-
Question 12 of 14
12. Question
12、7 个同学围坐一圈,要选 2 个不相邻的作为代表,有_________种不同的选法。 (2013年普及组)
-
有 种选法
CorrectIncorrect -
-
Question 13 of 14
13. Question
13、把 M 个同样的球放到 N 个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的放置方法?(用 K 表示)。
例如,M=7,N=3 时,K=8;在这里认为 (5,1,1)(5,1,1) 和 (1,5,1)(1,5,1) 是同一种放置方法。问:M=8,N=5 时,有多少种放置方法。(2014年普及组)
-
K=
CorrectIncorrect -
-
Question 14 of 14
14. Question
14、由数字1, 1, 2, 4, 8, 8 所组成的四位数的个数是( ) (2014年提高组)
-
答案为:
CorrectIncorrect -