笛卡尔树(Cartesian tree)
适用组别:提高组
难度系数:7
P5854
笛卡尔树是这样的一棵二叉树:首先,它是一个最小堆,即除了根结点,每个节点的权值都大于父节点的权值;其次,它的中序遍历恰好就是给定的序列。 笛卡尔树也可以是最大堆,逻辑相应改变。
笛卡尔树是一棵二叉树,树的每个节点有两个值,一个为key,一个为value。光看key的话,笛卡尔树是一棵二叉搜索树,每个节点的左子树的key都比它小,右子树都比它大;光看value的话,笛卡尔树有点类似堆,根节点的value是最小的,每个节点的value都比它的子树要小。
例题:
下图就是一棵对应的笛卡尔树。现输入序列的规模n(1≤n<100) 和序列的 n 个元素,试求其对应的笛卡尔树的深度 d(根节点深度为 1),以及有多少个叶子节点的深度为 d。
实例序列:
7 2 12 1 10 5 15 3
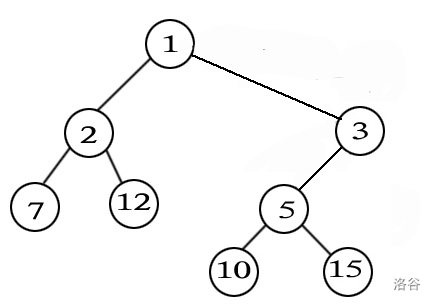
代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | /**************************************************************** * Description: C++ implementation of Cartesian tree 笛卡尔树 * Author: Alex Li * Date: 2023-07-06 13:02:29 * LastEditTime: 2023-07-06 13:11:50 ****************************************************************/ #include <iostream> using namespace std; const int SIZE=100; const int INFINITY=100000; int n,a[SIZE], maxDeep,num; void Solve(int left, int right, int deep){ int i,j,min; if(deep>maxDeep){ maxDeep=deep; num=1; } else if(deep==maxDeep)num++; min=INFINITY; for ( i =left; i <=right; i++) if(min>a[i]){ min=a[i]; j=i; } if(left<j)Solve(left,j-1,deep+1); if(j<right)Solve(j+1,right,deep+1); } int main(){ cin>>n; for (int i =1; i <=n; i++) cin>>a[i]; maxDeep=0; Solve(1,n,1); cout<<maxDeep<<' '<<num<<endl; } /* intput: 8 7 2 12 1 10 5 15 3 output: 4 2 */ |
I4585